شرح محيط المستطيل نقدمه لكم من خلال قمالنا هذا كما نذكر لكم محيط المربع هذا بالإضافة إلى ومساحة المستطيل كل هذا وأكثر تجدونه في ذلك الموضوع والختام خصائص المستطيل.
شرح محيط المستطيل
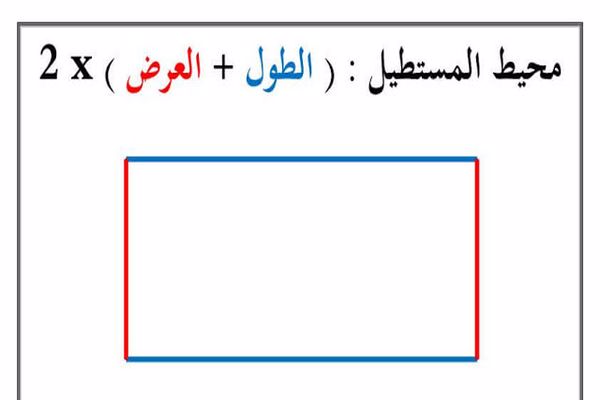
تعريف قانون محيط المستطيل
المستطيل هو أحد الأشكال الهندسية رباعية الأضلاع في الرياضيات، ويكون في المستطيل ضلعين متوازيان متقابلين ومتساوين من حيث الطول، وكل أركانه واقفة؛ حيث أن قياس كل ركن من أركان هذا المستطيل تعادل تسعين درجة، ويسمي أضلاع المستطيل الطول والعرض، ويعتبر أن المربع هو شيء أخر غير المستطيل؛ وذلك لأنه يكون الطول والعرض به متساويان والمحيط بشكل عام يعرف بأنه مقياس المسافة الخارجية التي تلتف بالشكل الهندسي، وبتوضيح أخر، المحيط هو طول الخط الذي يلتف بالشكل ثنائي الأبعاد مثل: المربع، أو الدائرة، أو المستطيل، وفي موقف المستطيل من الممكن أن نقول أن محيط المستطيل هو المجموع من أطوال أضلاعه ويطلق علي محور المستطيل باللغة الإنجليزية Rectangle Perimeter.
قياس محيط المستطيل
اكتب المعادلة
للبدء اكتب المعادلة الأساسية لإيجاد حجم المستطيل، ستساعدك هذه المعادلة في حساب محيط المستطيل: المحيط = 2 (الطول + العرض) والمحيط هو دائمًا المسافة الإجمالية على طول الحواف الخارجية لأي شكل بسيط أو معقد، في هذه المعادلة نشير إلى المحيط بالرموز “m” و “i” لطول المستطيل، والرمز “p” لعرضه، دائمًا ما تكون قيمة الطول أكبر من قيمة العرض ويكون الاثنان متساويين مع عرض المستطيل بسبب الأضلاع المتساوية المتقابلة.
أوجد طول وعرض المستطيل
تحدد مسألة الرياضيات العادية كلاً من طول وعرض المستطيل في المسألة، ومع ذلك في الحياة العادية يمكنك استخدام مسطرة أو مقياس أو شريط قياس لتحديد طول وعرض المنطقة المعالجة، اتخاذ إجراءات عند القياس في منطقة مفتوحة، قم بقياس جميع الجوانب لمعرفة ما إذا كانت الاتجاهات متوافقة حقًا ثم يتم ضرب مجموع الطول والعرض في 2 عند الانتهاء من هذه الخطوة ستحصل على محيط المستطيل وستأخذ عملية الضرب في الاعتبار ضلعي المستطيل الآخرين، عندما تجمع بين العرض والارتفاع، فإنك تقوم فقط بتوصيل جانبين من الشكل.
-ونظرًا لأن ضلعي المستطيل الآخرين يتوافقان مع الضلعين اللذين أضفتهما بالفعل، يمكنك مضاعفة هذا القياس للحصول على مجموع الأضلاع الأربعة على سبيل المثال، المحيط = 2 * (الطول + العرض) = 2 * (14 + 8) = 2 * (22) = 44 سم وختامًا ما هو قانون محيط المستطيل؟ إذا كنت تعرف طول وعرض المستطيل، فإن محيط المستطيل = طول الضلع الأول + طول الضلع الثاني + طول الضلع الثالث + طول الضلع الرابع، نظرًا لأن الضلعين متناسبان نفس الشيء، يمكن كتابة قانون المستطيل الذي له نفس الطول على النحو التالي: محيط المستطيل = 2 × الطول + 2 × العرض ، وفي الرموز: H = 2 × A + 2 × B حيث: A: العرض.
محيط المربع
(Square)، هو شكل من الأشكال الهندسية الرباعية ثنائية الأبعاد، ولا يمكن حصر استخدامات المربع في مختلف نواحي تطبيقات الحياة، حيث لا يقتصر استخدامه في مجال الرياضيات فقط، بل إنه يستخدم في كثير من المجالات العملية، وفي محيط حياة الأفراد اليومية، هذا ويعتبر المربع شكلًا هندسيًا مغلقًا، يمكن تقسيمه إلى مثلثين متساويين ومتماثلين، ويمكن حساب طول قطر المربع عن طريق استخدام نظرية فيثاغورث ومحيط المربع يعني مجموع المسافة التي يتم قطعها من نقطة ابتداء المربع مرورًا بجميع الأضلاع كاملًة، حتى العودة إلى نقطة البداية مرة أخرى. حيث إن جميع أضلاع المربع متساوية في الطول، فإن قانون محيط المربع يساوي مجموع كل أطوال أضلاع المربع، أي أن محيط المربع= 4 × طول الضلع.
مساحة المستطيل
يمكن تعريف المستطيل بالإنجليزية Rectangle بأنه عبارة عن متوازي أضلاع زواياه الأربعة قوائم، وهذا يعني أنّ كل مستطيل هو متوازي أضلاع، ولكنّ ليس كل متوازي أضلاع هو مستطيل، ويمكن إيجاد محيط المستطيل من خلال استخدام القانون الآتي:
محيط المستطيل = 2×الطول 2×العرض، وبالرموز: محيط المستطيل = 2×(ل ع).
أما بالنسبة لمساحة المستطيل فهي تُعطى بالعلاقة الآتية:
مساحة المستطيل = الطول×العرض، وبالرموز: مساحة المستطيل = ل×ع.
ومن الجدير بالذكر هنا أن مفهومي المحيط بالإنجليزية Perimeter والمساحة بالإنجليزية Area ويعتبران من أهم المفاهيم في علم الرياضيات؛ حيث تعبّر المساحة عن مقدار المادة اللازمة لتغطية الشكل ثنائي الأبعاد من الخارج، وتُقاس بالوحدات المربعة مثل: الإنش المربع، والسنتيمتر المربع، والميل المربع، وغيرها، أما المحيط فيصف المسافة المحيطة بالشكل ثنائي الأبعاد، ويعادل مقدار المحيط عادة طول الخيط الذي يمكن لفّه حول حدود الشكل ثنائي الأبعاد، كما أنّ المسافة المقطوعة عند السير حول حديقة المنزل لمرة واحدة مثلاً يعادل محيط الحديقة هذه الحديقة، ويُمكن إيجاد المحيط لأي شكل منتظم من خلال إيجاد مجموع أطوال أضلاعه، وهو يُقاس عادة بالوحدات الخطية؛ مثل الإنش، والسنتيمتر، والقدم، وغيرها، ويجب التأكد دائماً من أن الوحدة المستخدمة لقياس كل من الطول والعرض هي ذاتها عند حساب المحيط أو المساحة.
محيط المربع
يعرف المحيط لأي شكل مغلق بأنه المسافة المحيطة بالشكل، ويمكن إيجاد محيط المربع Square Perimeter عن طريق حساب مجموع أطوال أضلاعه الأربعة، ولأن جميع أضلاع المربع متساوية في الطول، فإنه يمكن إيجاد محيطه باستخدام القانون الآتي:
-عند معرفة طول الضلع: محيط المربع = 4×طول الضلع، وبالرموز: ح=4×س؛ حيث:
ح: محيط المربع.
س: طول الضلع.
-عند معرفة طول القطر: يمكن كذلك في حال معرفة طول أحد قطري المربع، إيجاد محيطه باستخدام العلاقة الآتية:
محيط المربع = 2×الجذر التربيعي للعدد 2×طول القطر، وبالرموز: ح=2×2√×ق؛ حيث:
ح: محيط المربع.
ق: طول قطر المربع.
خصائص المستطيل
1-كل ضلعين متقابلين متوازيين
2-فيه 4 زوايا قائمة (قيمة الزاوية الواحدة تساوي 90 ْ)
3-شكل هندسي ثنائي الأبعاد (طول وعرض)
4-يتكون المستطيل من 4 أضلاع
5-كل ضلعين متقابلين متساويين
6-مساحة المستطيل = الطول × العرض
7-قطراه متساويان و ينصف أحدها الآخر
8-محيط المستطيل = 2 × (الطول + العرض)